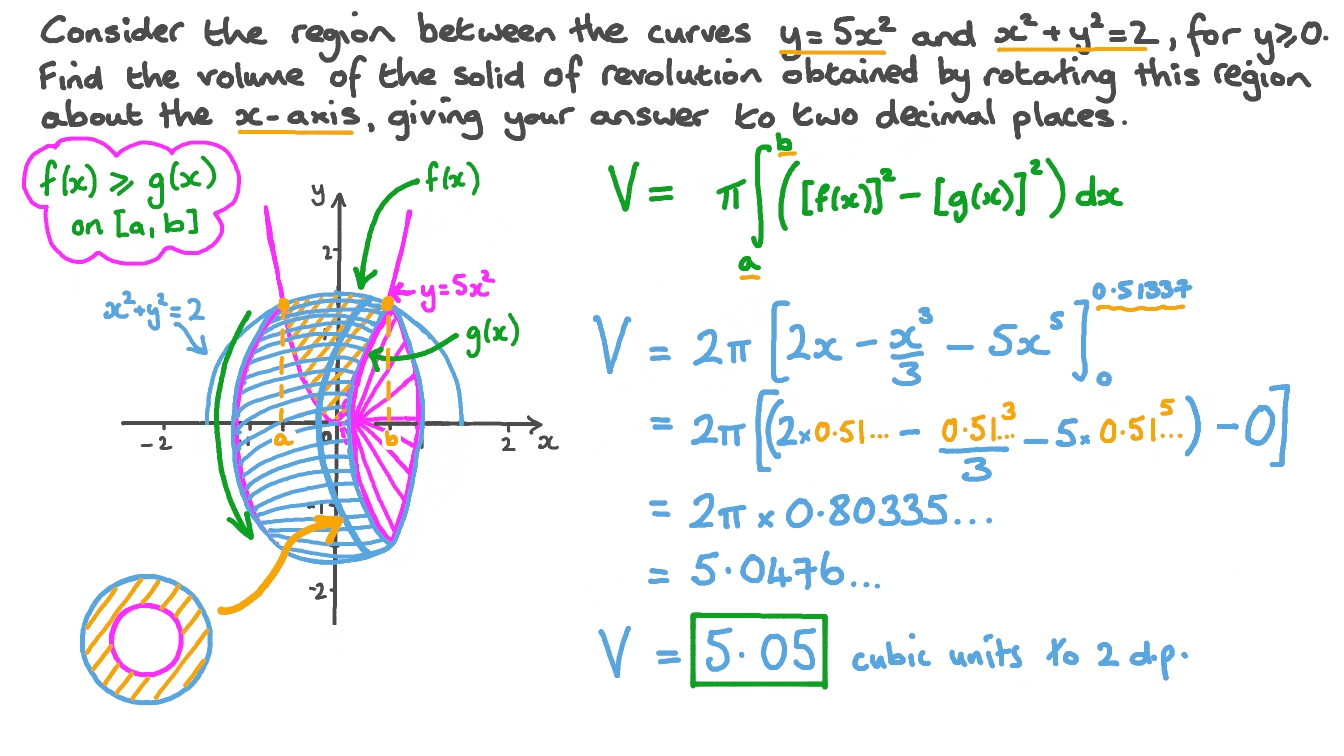
Question Video Finding The Volume Of A Solid Of Revolution Bounded By A Parabola And A Circle Nagwa
Web y = x is the line that passes through the origin with slope 1 The integral for the area is ∫4x −x2 − xdx = ∫3x −x2dx integrating we have 3 2 x2 − 1 3 x3 Evaluating at weWebIn the figure, the equation of the solid parabola is y = x2 8 and the equation of the dashed line is y = 7x Determine the area of the shaded region The area of the shaded region is
